Hans H. Diebner's Research

Lyapunov exponents

The so-called Lyapunov exponents are essential characteristics to describe the stability of dissipative systems. These entities are measures for the exponential divergence or convergence of neighbored trajectories of nonlinear systems. The importance of the Lyapunov exponents results from the fact that an exact measurement of the actual state is virtually impossible. In chaotic systems this uncertainty usually increases exponentially with time which is why predictability is reduced (a well-known example is the weather dynamics). This is why Lyapunov exponents are a particular useful measure for predictability.

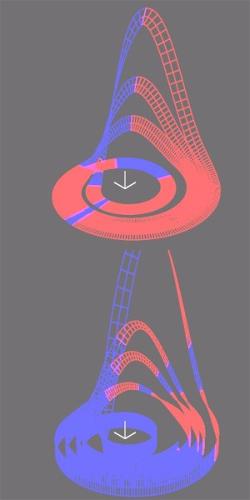
We work on the improvement of the numerics for the estimation of these important entities since it has turned out that commonly used methods are insufficient. The upper figure to the right shows the so called positive manifold of the Rössler attractor. Within the attractor the local Lyapunov exponents are almost everywhere positive (red band) which is why a small area of states grows exponentially in time. Orthogonal to the attractor, in contrast, the exponents are almost everywhere negative (blue band in the lower figure) which is why the attractor attracts points from the outside. I am grateful to Florian Grond for his collaboration in this project in form of a final year project. Together with Florian and others, I published the following papers on Lyapunov Exponents:

Florian Grond, Hans H. Diebner, Sven Sahle, Adolf Mathias, Sebastian Fischer and Otto E. Rossler: A robust, locally interpretable algorithm for Lyapunov exponents. Chaos, Solitons & Fractals 16, 841-852 (2003). (pdf)
Florian Grond and Hans H. Diebner: Local Lyapunov Exponents for Dissipative Continuous Systems. Chaos, Solitons & Fractals 23, 1809-1817 (2005). (pdf)