Hans H. Diebners Forschung
Lyapunov-Exponenten
 Wesentliche Charakteristika der Stabilität dissipativer Systeme stellen die so genannten Lyapunov-Exponenten dar. Sie sind ein Maß für das exponentielle Auseinanderdriften bzw. Konvergieren von benachbarten Trajektorien eines nichtlinearen Systems. Die Bedeutung resultiert aus der Tatsache, dass in praxi nie eine völlig exakte Messung eines Zustandes vorgenommen werden kann. Bei chaotischen Systemen sorgt ein oder mehrere positive Lyapunov-Exponenten dafür, dass sich die Messunsicherheit sehr schnell ausweitet, was eine Prädiktion sehr schwierig gestaltet (bekanntes Beispiel: Wetterdynamik). Die Lyapunov-Exponenten stellen daher ein ausgezeichnetes Maß für die (Un-)Vorhersagbarkeit dar.
Wesentliche Charakteristika der Stabilität dissipativer Systeme stellen die so genannten Lyapunov-Exponenten dar. Sie sind ein Maß für das exponentielle Auseinanderdriften bzw. Konvergieren von benachbarten Trajektorien eines nichtlinearen Systems. Die Bedeutung resultiert aus der Tatsache, dass in praxi nie eine völlig exakte Messung eines Zustandes vorgenommen werden kann. Bei chaotischen Systemen sorgt ein oder mehrere positive Lyapunov-Exponenten dafür, dass sich die Messunsicherheit sehr schnell ausweitet, was eine Prädiktion sehr schwierig gestaltet (bekanntes Beispiel: Wetterdynamik). Die Lyapunov-Exponenten stellen daher ein ausgezeichnetes Maß für die (Un-)Vorhersagbarkeit dar.
Mit meinem Team trugen wir dazu bei, die Numerik der Berechung dieser wichtigen Kenngrößen zu verbessern, da es sich gezeigt hatte, dass die bisherigen Methoden unzulänglich waren. Unser neu entwickelter Algorithmus zur Berechnung der Lyapunov-Exponenten beruht auf einem einfachen selbstevidenten Prinzip. Entlang der Trajektorie, also in longitudinaler Richtung, kann es im Mittel keine Dissipation geben, sonst könnte ja ein etwas später gestarteter Zustand den vorhergenden auf derselben Trajektorie überholen. Falls die Trajektorie später wieder in beliebiger Nähe zum initialen Zustand vorbeikommt, gewährleistet unser Algorithmus, dass auch die gleichen lokalen Beiträge zum Lyapunov-Exponenten beliegig genau reproduziert werden. Dies ist nur dann der Fall, wenn man die gelegentlich notwendigen Renormalisierungen bei der Berechung der Lyapunov-Exponenten immer entlang der longitudinalen Richtung vornimmt. Im Gegensatz zu anderen Algorithmen sind so nicht nur die globalen Mittelwerte, sondern auch die lokalen Beiträge interpretierbar, weil konsistent.
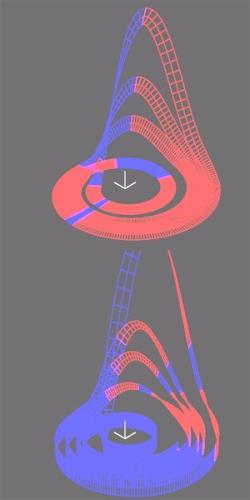
Unser Algorithmus liefert für ein dreidimensionales System (z.B. Rössler- oder Lorenz-System) in jedem Punkt ein lokales Dreibein, nämlich die Lyapunov-Mannigfaltigkeiten. Die logitudinale Achse des Dreibeins entlang der Trajektorie ist die neutrale "Null", d.h. die Beiträge mitteln sich im Laufe der Zeit zu Null. Eine zweite Mannigfaltigkeit ist die der maximalen Divergenz und schließlich gibt es eine Mannigfaltigkeit der maximalen Konvergenz. Diese Mannigfaltigkeiten sind in den Abbildungen für den Rössler-Attraktor zu sehen.
Das Bild links oben zeigt die sich aufweitende, also maximal divergierende Mannigfaltigkeit im Rössler-Attraktor. In den roten Bereichen, die innerhalb des Attraktors überwiegen, sind die lokalen Exponenten positiv. Hingegen überwiegen senkrecht zum Attraktor die negativen Lyapunov-Exponenten. Dies führt zu einer weitgehend blau eingefärbten Mannigfaltigkeit im Bild links unten. Dies erklärt, warum der Attrakor außenliegende Zustände attrahiert und die innerhalb des Attraktors liegenden Bereiche aber exponentiell unscharf werden lässt. Mein Dank gilt dem Kollegen Florian Grond, der in diesem Forschungsgebiet seine Diplomarbeit anfertigte. Zusammen mit Florian und anderen sind folgende Publikationen zur numerischen Berechnung von Lyapunov-Exponenten zustande gekommen:
Florian Grond, Hans H. Diebner, Sven Sahle, Adolf Mathias, Sebastian Fischer and Otto E. Rossler: A robust, locally interpretable algorithm for Lyapunov exponents. Chaos, Solitons & Fractals 16, 841-852 (2003). (pdf)
Florian Grond and Hans H. Diebner: Local Lyapunov Exponents for Dissipative Continuous Systems. Chaos, Solitons & Fractals 23, 1809-1817 (2005). (pdf)